I recently had the chance to work on a problem involving string pattern matching. One of my favorite aspects of programming is solving these sorts of algorithmic puzzles so I quite enjoyed working on this problem.

After working out my first solution involving lots of nested loops I decided to research a bit I came accross the Trie data structure. A trie can look very similar to a regular binary search tree as seen below (Trie: left Binary Tree: right) however there a few key differences.

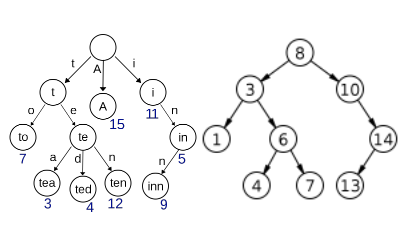
Although tries use a tree like structure they are different from a normal binary search trees for several reasons.

• Each descendent of a node all share a common prefix like “i” for “in” and “inn” in the above example. Because of this tries are often called “Prefix Trees”

• No node in the trie stores any key associated with that particular node, instead the location of the node in the tree defines what key with which each node is associated.

So now that we know that a trie is sufficently different from a regular binary search tree

Benefits

• Looking up data in a trie is faster than looking up data in an imperfect hash table ( O(m) with m being the length of the search string vs. O(N) )
  • An imperfect hash table is one with key collisions, instances in which the hash function maps different keys to the same position in a hash
  • Take a look at here to see why this is a problem in hashe’s and how they get around it
• A trie will not contain any key colisions
• Trie Buckets are only necessary if there are multiple values associated with the same key
• Adding and deleting items from a trie is simple

Drawbacks

• Trie lookups can take a longer time if the trie is stored on a hard disk and not in virtual memory
• Some tries require more space than equivelent hash tables
• Certain keys, like foating point numbers, do not provide much meaning and must be used with the Bitwise Trie implementation

So Why a Trie?

Tries are great for matching full and parital string patterns and can be used for predictive text, autocomplete, and even spell check. The matching algorithm is so good in a trie because the strings are organized by prefix, so a large amount of potentially searchable data can be safely ignored with just the first letter of a search term.

Given a trie matching function trie.match("tea") on the below trie(same as above but represented differently) only branches with the parent prefix “t” will be searched, which safely eliminates anything without that prefix.

1
2
3
4
5
6
7

{:root=>
  {"t"=>
    {true=>{},
     "o"=>{true=>{}},
     "e"=>{true=>{}, "a"=>{true=>{}}, "d"=>{true=>{}}, "n"=>{true=>{}}}},
   "A"=>{true=>{}},
   "i"=>{true=>{}, "n"=>{true=>{}, "n"=>{true=>{}}}}}}

Implementaions

In my next post I will build a simple trie implementation in Ruby.

Alternatively, if you cannot wait you can use the Trie Gem, one of the many Node packages, or whatever library you find best.